生物の運動を記述する微分方程式に魅せられて～細胞性粘菌やがん細胞の集中現象を数学的に解析する～ 千葉大学 大学院理学研究院 准教授 石田 祥子[ Sachiko ISHIDA ]

現実の現象を数式で記述する「偏微分方程式」。物理や化学をはじめ、さまざまな現象を表す偏微分方程式が提唱されており、多くの数学者がその性質を解明すべく研究に取り組んでいる。その中で、「生物の運動を表す偏微分方程式」に焦点を当てているのが、大学院理学研究院の石田祥子准教授だ。

「細胞性粘菌」や「がん細胞」の運動を記述する偏微分方程式について、その解の挙動を研究する傍ら、国際的な研究集会の代表としても精力的に活動をこなす。
「次々にやりたいことが出てきて忙しいが、それがすごく楽しい」と語る石田准教授に、研究内容や今後の展望を伺った。

細胞性粘菌が集まる様子を数学的に解析する

－最初に、先生のご研究について教えてください。

生物の動きにもさまざまな種類がありますが、中でも「走化性」という性質をもつ生物・細胞の運動を記述する偏微分方程式の数学解析が、私の研究テーマです。走化性とは生物が化学物質に引き寄せられて集まる現象で、免疫など私たちの体の中でも重要な働きをしています。

具体的には、生物の密度や化学物質の濃度を未知関数として、「自然に広がっていく運動（拡散）」と「走化性による運動（凝集）」の２つの特性をもつ(偏微分)方程式を考えます。方程式を解くことで、未知関数、つまり生物や化学物質の分布が求まりますが、方程式が複雑なため、解が明確に表せるとはかぎりません。私は、解が時間とともにどう変化するのか、つまり、時間が進むにつれて生物や化学物質の分布がどう変わるのかを数学的に調べています。

－具体的にはどのような偏微分方程式を研究されているのですか？

主に２つの偏微分方程式を研究対象としています。

一つ目は、細胞性粘菌の集中現象を表す「ケラー・シーゲル系」です。細胞性粘菌は普段は単体（単細胞）で生活していますが、飢餓状態になると各個体が化学物質を放出して場所を教え合い、10万以上の個体が一カ所に集合して多細胞になります。この集合過程を、ケラー・シーゲル系は２本の偏微分方程式^*により記述しています。

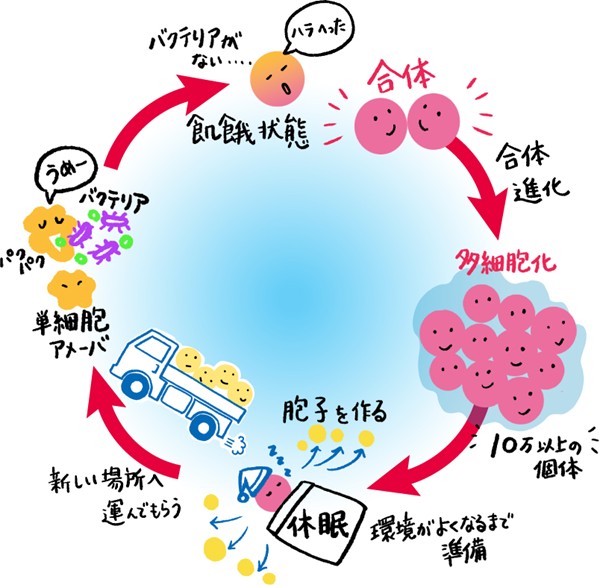
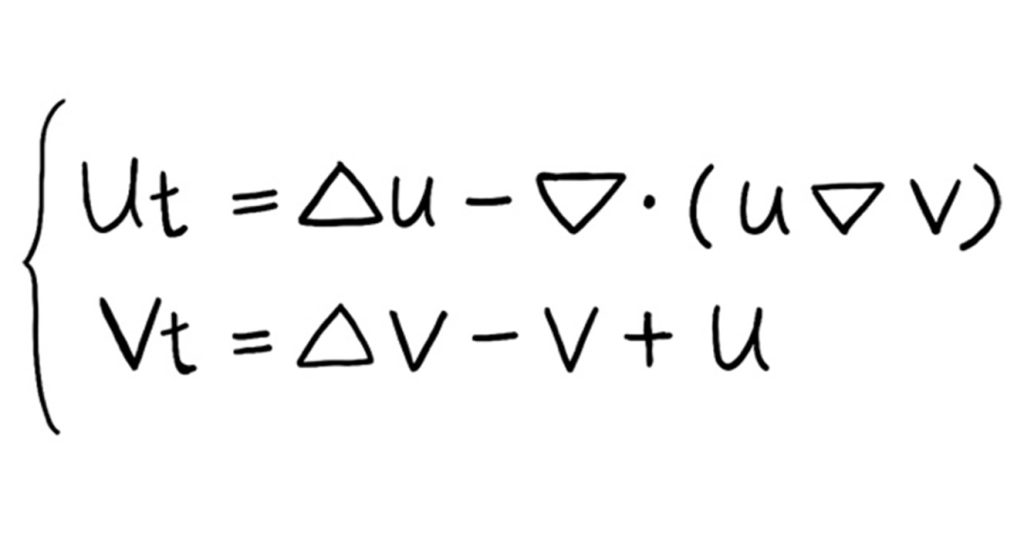
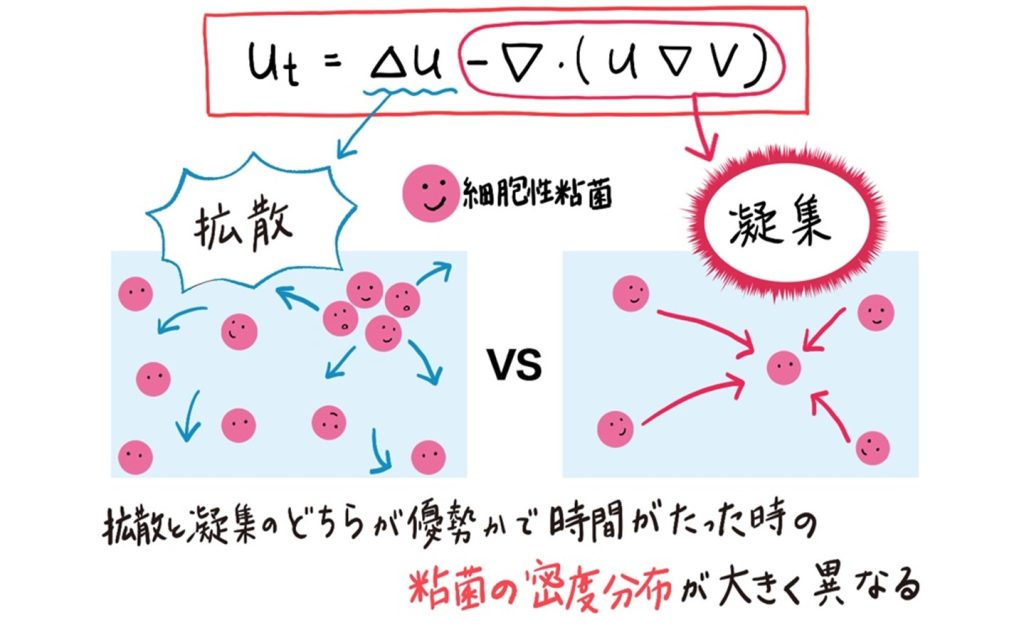
ケラー・シーゲル系の面白さは、「拡散」と「凝集」を表す２つの項をもつ点です。この２つの項のバランスにより、時間が経過した後の粘菌の密度を表す関数の形状が異なります。例えば、適切な条件下で凝集の力が大きければ粘菌はどんどん集まってきて、１点で無限大に密集します（解の爆発）が、逆に拡散の影響が大きければ解の爆発はおきません。では、どのような挙動を示すのか？

―このような数理構造を調べて論文として報告しています。

ケラー・シーゲル系の研究を始めたきっかけをお聞かせください。

修士課程１年次の終わりに、恩師である横田智巳先生^*1から「どんな研究に興味がありますか」と尋ねられました。横田先生は、東京理科大学で開催されている神楽坂解析セミナーをはじめ、さまざまな研究集会へ参加する機会を学生に多く設けてくださったのですが、その中でいろいろな方の講演を聴いていくうちに、興味をもったものが「生物モデル」でした。そのことを横田先生に伝えると、すぐにケラー・シーゲル系の研究を精力的にされていた杉山由恵先生^*2へコンタクトをとってくださり、研究集会に杉山先生を講演者として招いてくださいました。このご講演をきっかけに、ケラー・シーゲル系に関する研究をスタートしました。

当時、私は修士１年でしたので杉山先生のご講演内容のほとんどを理解していなかったと思いますが、杉山先生が楽しそうに講演する姿に憧れのような気持ちを抱いたことも、研究を始めるきっかけの一つだったかもしれません。

*1: 解析学（偏微分方程式）を専門とする東京理科大学理学部第一部の教授（2025年5月現在）
*2: 非線形偏微分方程式論を専門とする大阪大学大学院情報科学研究科の教授（2025年5月現在）

修士・博士課程では、準線形拡散ケラー・シーゲル系の解析に取り組みました。特に、「時間無限大まで解が存在するような拡散と凝集のバランス」に関する予想の解決を目指し、試行錯誤を重ねていました。一歩一歩……いえ、1/10歩でも前に進めば大成功！というような毎日でした。最大正則性原理という評価式を用いることで問題解決への道筋が見えた日のことは強く印象に残っています。

時間無限大まで解が存在することがわかった後は、「解は時間無限大まで有界か、それとも時間無限大で爆発するのか」・「解は時間無限大でどのような関数に収束するか」・「有限時間で解が爆発するような拡散と凝集のバランスはどのようなものか」といった問に取り組みました。それぞれの研究成果を論文としてまとめ、国際誌に発表しています。

がん細胞の広がりを記述する偏微分方程式を、先駆者として研究

－もう一つの研究対象についても教えてください。

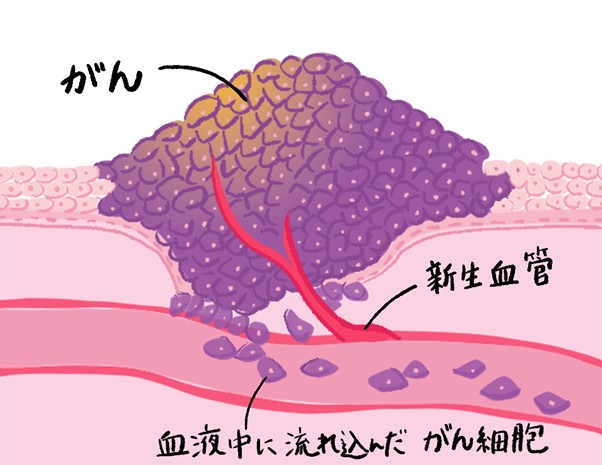
2つ目の研究対象は「がん浸潤モデル」と呼ばれる、がん細胞が周囲の組織に広がる様子を記述した偏微分方程式です。
がん細胞はタンパク質分解酵素を分泌することで、周囲の正常な組織を破壊しながら徐々に移動していきます。この現象を「浸潤」といいます。ここでは、タンパク質分解酵素の作用によりがん細胞を誘引する物質が新たに生成され、それにより効率的に浸潤が進行するという仮説のもと提唱されたモデルについて考えます。

がん浸潤モデルは、ケラー・シーゲル系と同じように「拡散項」と「凝集項」をもつ連立微分方程式ですが、方程式の数が4つに増えるため、解析の難易度は各段に高くなります。拡散と凝集のバランスもケラー・シーゲル系とは異なることが分かってきて、非常に興味深いです。現在も、共同研究者である横田先生と毎週のようにホワイトボードを囲みながら、頭を突き合わせて議論を交わしています。

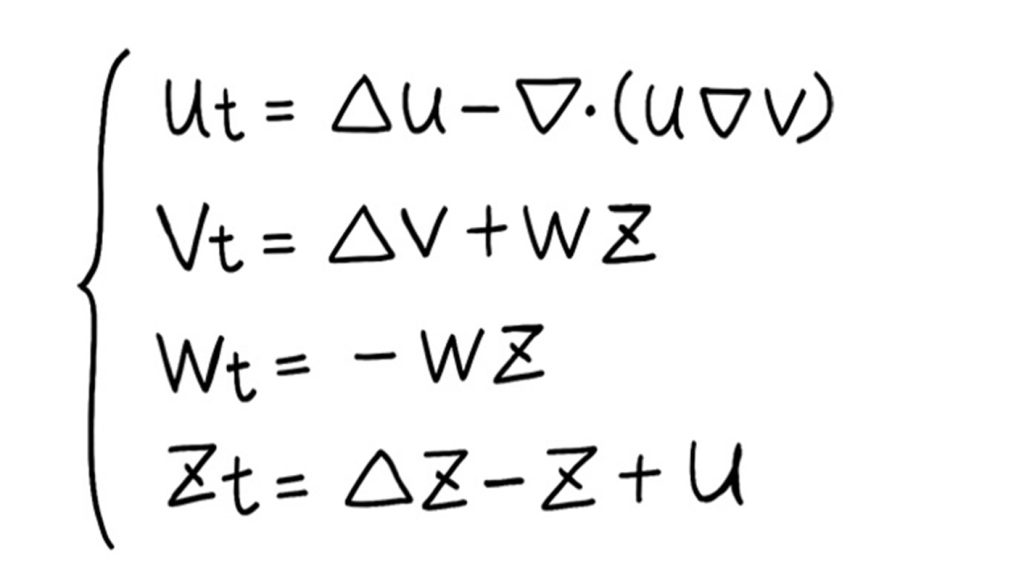
「このままでは終われない！」という強い気持ちで研究者の道へ

－先生はなぜ数学の研究者になろうと思ったのですか？

元々、大学卒業後は高校の数学の教員になろうと考えていました。転機になったのは、大学3～4年生のときに履修したゼミです。ゼミを通し、わからないことを理解する過程がとても面白いと感じました。同時に、それまで大学で学んできた内容は、数学全体のほんの一部なのだと気づかされました。「数学の世界は想像以上に広く豊かで、自分はその入り口に立ったばかり。もっと勉強して、数学に対する手応えを感じなければとても卒業できない」と強く思い、大学院への進学を決意しました。大学院生の間は横田先生のご指導の下、同期との自主ゼミを行ったり、先輩方もゼミに長時間付き合ってくださったりと、恵まれた環境で学ぶことができたと思います。

数学の研究には終わりがありません。研究を進める中でやりたいことが次々と出てきますし、研究発表の場でいただいた質問がきっかけで、新たな課題に気づくこともあります。取り組みたい研究テーマが常に頭の中にあふれている状態で、一つ一つ丁寧に向き合っているところです。解決への糸口を見つけた時にはうれしくなります。特に、長く悩んでいた問題が解決したときはうれしさのあまり、思わずスキップしたくなりますね。

－先生は、国際的な研究集会も開催されていると聞きました。

はい、走化性モデル（ケラー・シーゲル系やがん浸潤モデルなどの総称）に関連する研究成果を挙げている研究者を世界中からお招きして、年に一度、国際研究集会を主催しています。2022年はドイツ、2023年は日本、今年はイタリアで開催しました（2025年5月現在）。細々とした事務手続きは大変な面もありますが、講演をご快諾いただけるとありがたく、研究成果の講演内容は私にとっても大変学びの多いものとなっています。現在は、多くの方にこの集会に興味を持ってもらえるよう、工夫をして頑張っているところです。こうした国際交流を通して新たな研究テーマや共同研究が生まれることもありますから、今後も続けていきたいと考えています。

「数学にじっくり向き合う」ことが将来の力となる

今後共同研究をしたい分野はありますか？

偏微分方程式の数値解析（シミュレーション）を行っている先生と共同研究がしたいですね。私は紙とペンのみを使って偏微分方程式を数学的に解析していますが、PCで近似的にシミュレーションすれば、新たな視点が得られるのではと考えています。

－最後に、学生へのメッセージをお願いします。

「じっくりと数学に向き合うこと」ーこれが何よりも大切だと思います。例えば、教科書を読むときは、何となく読み進めるのではなく、全ての行とそれらの行間までも説明できるようになるまで丁寧に読み込み、しっかりと理解してください。どうしてもわからない点があれば、「どこまでわかっていて、どこからわからないのか」を明確にしてから質問しにきてくれると、より充実したディスカッションができます。

時間はかかりますが、そうやって真摯に数学と向き合った経験はあなたの財産となるはずです。私もまだまだ道半ばです。ともに一歩一歩、じっくり数学に取り組んでいきましょう。

● ●　Off Topic　● ●