Contents
Share
Imagine the movement of waves, the transmission of radio waves, and even the way leaves fall from trees. If I tell you these familiar phenomena can all be captured and expressed through mathematical formulas, would that surprise you?
These everyday phenomena find their mathematical representation in the form of partial differential equations, which are recognized as fundamental formulas that depict various physical processes. Associate Professor Masaya Maeda, hailing from the Graduate School of Science at Chiba University, is on a quest to unlock the secret held within these equations.
Associate Professor Maeda dives into studying the behavior of ‘mysterious waves’ known as ‘solitons,’ which emerge during the analysis of specific partial differential equations. His research findings have gained significant recognition for partially solving a longstanding issue within the mathematics world. In acknowledging his contributions, he was awarded the Minister of Education, Culture, Sports, Science and Technology Commendation in 2020, as well as Chiba University’s Award for Distinguished Researcher in 2022. We had the opportunity to converse with Associate Professor Maeda, who persistently pursues his scholarly endeavors, and discussed his perspectives on research and education.
Unraveling physical phenomena from the rigorous viewpoint of mathematics
――Why did you start studying mathematics?
Since childhood, I have been fascinated by nature and the cosmos, which led me to enroll in the Faculty of Science at Kyoto University. Initially, I intended to major in physics. However, as time passed, I realized a strong affinity for mathematics’ precision and logical thinking. This realization prompted me to redirect my focus to the field of mathematics during my junior year.
Nevertheless, my interest in physics persisted. As a result, in the fourth year, I chose to join a laboratory specializing in ‘mathematical physics,’ an approach that examines physics from a mathematics standpoint. Professor Yoshio Tsutsumi is a distinguished authority in partial differential equations. Naturally, my involvement with this laboratory also took me to the realm of partial differential equations.
――What exactly are partial differential equations?
To put it simply, a partial differential equation is a mathematical expression that represents the rules of physical phenomena. The movement of the waves on water surfaces, the descent of a falling ball, the patterns of wind. All these everyday physical occurrences can be described using partial differential equations.
Now, how do these equations actually dictate the movement of waves or determine the time a ball takes to hit the ground? We must solve the partial differential equations and obtain their solutions to understand these specific behaviors. However, some of these equations are unsolvable in the sense that they cannot be expressed using familiar functions like polynomials, trigonometric functions, or exponentials. This aspect of studying the behavior of unsolvable partial differential equations is a significant focus within mathematics.
My research revolves around the ‘nonlinear Schrödinger equation,’ which is generally considered an unsolvable partial differential equation, and its representative solution is known as the ‘soliton.’
Succeeded in Partial Verification of ‘Soliton Resolution Conjecture’
――What is a ‘Soliton’?
A soliton is a peculiar wave that exists in isolation. While ordinary waves lose shape as they travel, solitons maintain a consistent speed and shape over long distances. They are a common solution within a class of partial differential equations, including the nonlinear Schrödinger equation.
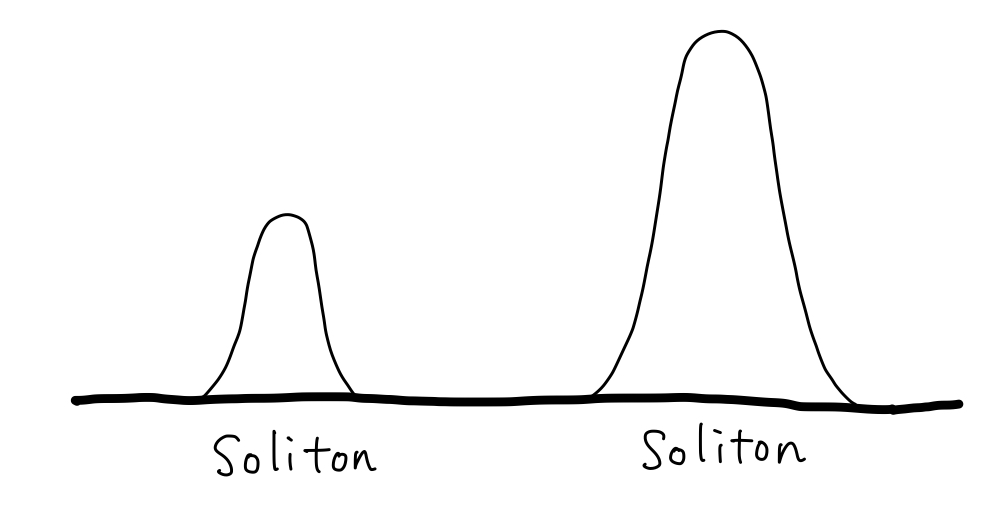
Despite their seemingly unusual behavior, solitons are observed in various physical phenomena. For example, on a daily scale, they appear as shallow water waves. On a microscopic scale, they present light propagation within an optical fiber. Zooming out on a larger scale, we can see their presence in cyclone movement, atmospheric gusts, and even the dynamics of black holes in space. Solitons remain hidden throughout the fabric of our world.
――You mean, this soliton is expected to represent a ‘behavior of general solutions’ for the ‘nonlinear Schrödinger equation’
That’s right. This is known as the ‘Soliton Resolution Conjecture.’ Proving this resolution is a significant goal among researchers in this field, and I have been working on it for numerous years.
To prove the soliton resolution conjecture, it is crucial to demonstrate that the soliton appears as a valid ‘solution’ and maintains an unchanging shape. The two concepts come into play: ‘stability’ and ‘asymptotic stability’ of solitons.
“Stability” refers to the property where the shape of the soliton solution remains largely intact without significant distortion. ‘Asymptotic stability’ is a concept that extends beyond stability, indicating the characteristic of a stable soliton where its oscillation diminishes, leading to the preservation of its shape. Resolving the soliton resolution conjecture necessitates demonstrating the entire process where all solutions approach the soliton, and the soliton solution becomes ‘asymptotically stable.’
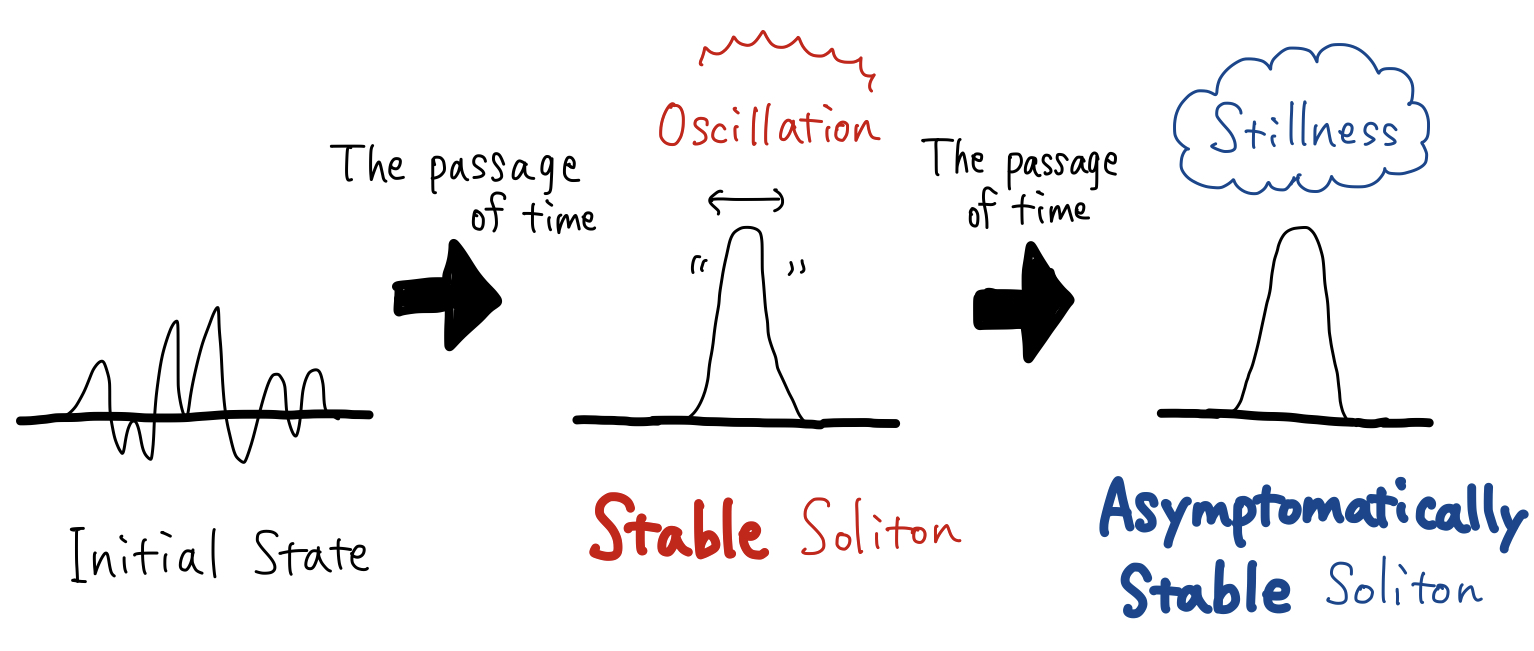
――I see. Is all of this process currently proven?
The ultimate goal is to achieve that, but the present situation is quite challenging within modern mathematics. It would be surprising if I could accomplish the proof within the next 25 years before my retirement. As a result, my research focuses on the process in which stable solitons are actually asymptotically stable.
At this point, I have succeeded in proving the asymptotic stability of solitons with certain oscillation patterns. This proof has received substantial recognition due to its applicability to a relatively diverse array of solitons. For this reason, I was honored to receive the Commendation from the Minister of Education, Culture, Sports, Science and Technology in 2020. In the future, my plan involves continuing my research to encompass solitons with even more varied vibration patterns.
The exploration of soliton stability and asymptotic stability might also lead to practical applications, such as stabilizing light within optical fibers to extend transmission distances. Personally, I find the mathematical analysis of solitons intriguing. Nevertheless, I would be grateful if someone could put my research findings into practice for societal implementation.
Studying “equations with rich structure” that nature endows
――What factors do you consider when deciding on a research theme?
I’m interested in studying ‘equations expected to exhibit rich mathematical structure.’ For instance, equations that capture natural phenomena. The Navier-Stokes equation, which expresses fluid motion, has been studied for nearly 200 years. Even now, it yields remarkable mathematical discoveries and is a crucial tool for explaining phenomena like ocean currents and atmospheric dynamics. Nature truly provides us with intriguing models that are well worth investigating.
However, in physics, there are cases where equations that appear to be good candidates for representing natural phenomena, form a mathematical perspective, and result in ‘solutions’ that diverge or become unstable, rendering them inadequate for accurately depicting these natural occurrences. Such equations are also captivating.
――You mentioned having a prior interest in physics, and it seems you maintain a connection to physics when choosing your research themes
Indeed. Additionally, I tend to steer clear of fields that are heavily saturated with researchers. I’m not particularly fond of intense competition. As a result, my approach involves selecting topics that haven’t been extensively explored, allowing me to delve deeply into them and study their intricacies thoroughly.
The delight of mathematics comes from thoroughly contemplating what captivates you
――I think many people feel they are not skilled at mathematics. How can such individuals come to appreciate the joy of mathematics?
One of the factors leading to an aversion to mathematics might be rooted in their childhood experiences. During childhood, the pressure to ‘accurately solve given problems within a short time’ for tests and exams is prevalent. It’s no wonder that mathematics becomes disliked under such circumstances.
However, the true essence of mathematics lies in a completely different realm. Mathematics is a discipline where you spend a day, two days, or even a year pondering problems that interest you. If this perspective could be widely communicated, I believe more and more people could be freed from childhood curses and develop an affection for mathematics.
――Finally, please give a message to students who find interest in your research
Primarily, I encourage students to prioritize what they enjoy and are curious about in their research pursuits. I want them to take the time to engage with their interests and discover a research topic that they can commit to for a long time.
However, in mathematics, it is quite common not to grasp the entirety of a field just by superficially exploring its facets. Hence, finding a research theme on their own might be challenging initially. At the outset, I recommend following the guidance of their academic supervisor, reading books and papers as instructed, and through the process of investigating the designated field, they’ll naturally uncover areas that genuinely intrigue them.
Ultimately, it would bring me great satisfaction if students could openly tell me, ‘Your research is boring’ or ‘Mine is more fascinating.’ Together, let’s cultivate an environment where we can revel in the joys of mathematics and explore its profound world. I’m eagerly awaiting individuals who embrace this joy.
