Differential Equations for Living Organisms: Modeling the Movement of Cellular Slime Molds and Cancer Cells Associate Professor, Graduate School of Science, Chiba University Sachiko ISHIDA

Partial differential equations are mathematical tools used to describe real-world phenomena. They have been applied to model a variety of processes in physics and chemistry, and many mathematicians are working to understand their properties in depth. Among them, Associate Professor Sachiko Ishida of the Graduate School of Science focuses on partial differential equations that describe the movement of living organisms.

While studying the behavior of solutions to partial differential equations that model the movement of cellular slime molds and cancer cells, Dr. Ishida is also actively involved as a representative at an international research conference.
“I’m busy because new things I want to do keep coming up, but it’s a lot of fun,” she says with a smile. We spoke with Dr. Ishida about her research and her vision for the future.

Mathematical analysis of cellular slime mold aggregation

Could you start by telling us about your research?

There are many different types of biological movement, but my research focuses on the mathematical analysis of partial differential equations that describe the movement of organisms and cells exhibiting a phenomenon known as ‘chemotaxis.’ Chemotaxis is the process by which organisms are attracted to and aggregate around chemical substances, and it plays an essential role in the body, including in the immune system.

Specifically, we study a partial differential equation with two key components: ‘natural spreading movement (diffusion)’ and ‘chemotactic movement (aggregation),’ where the density of organisms and the concentration of chemicals are the unknown functions. By solving the equation, we can determine these unknown functions—that is, the distribution of organisms and chemicals. However, because the equation is complex, the solution cannot always be expressed explicitly. I am mathematically investigating how the solution evolves over time, meaning how the distribution of organisms and chemicals changes as time progresses.

More specifically, what types of partial differential equations are you studying?

My research mainly focuses on two types of partial differential equations.

The first is the Keller-Segel system, which describes the aggregation behavior of cellular slime molds. Normally, these organisms live as single cells, but when they experience starvation, each cell releases chemicals to signal its location to others. As a result, more than 100,000 individuals gather in one place to form a multicellular structure. The Keller-Segel system represents this aggregation process through two partial differential equations^*.

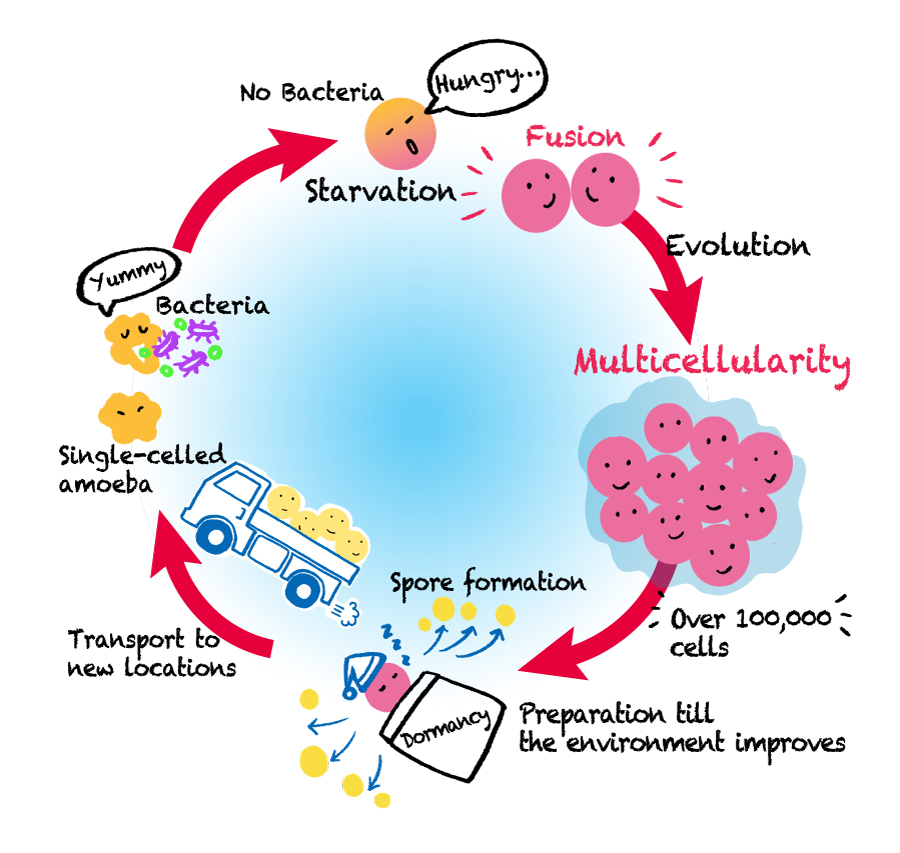
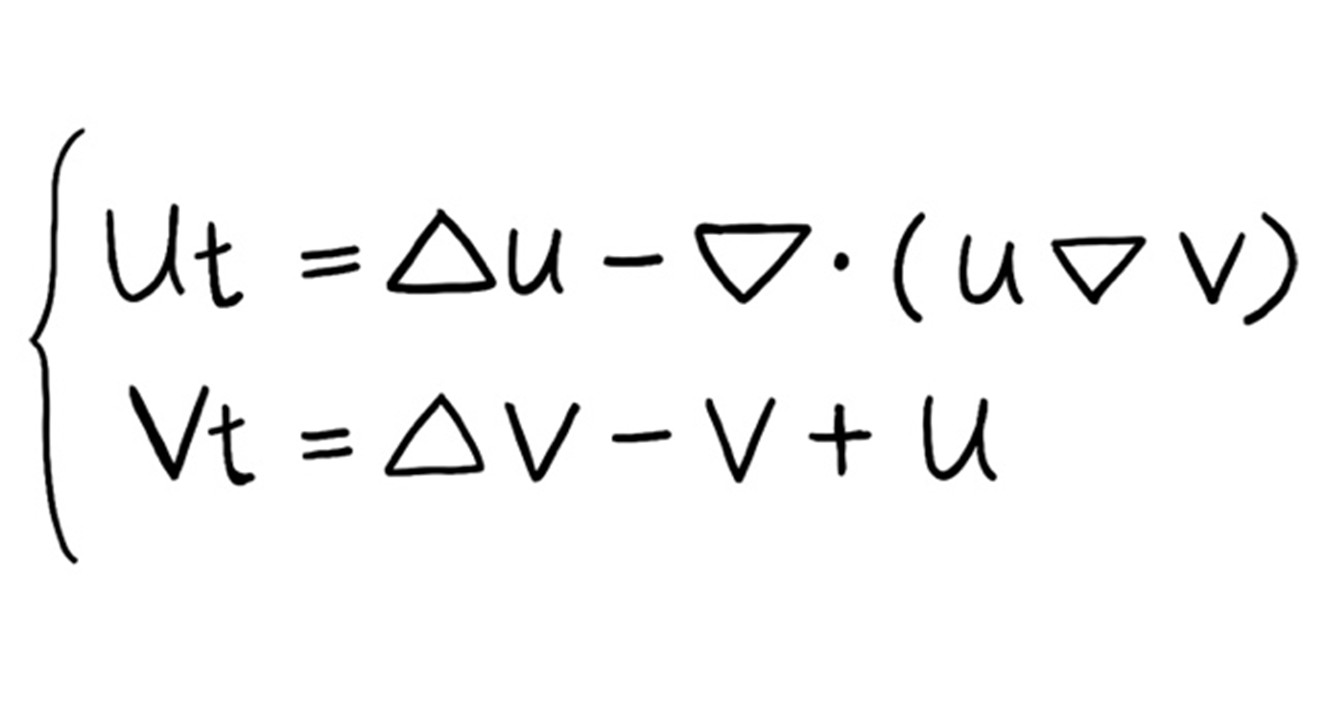
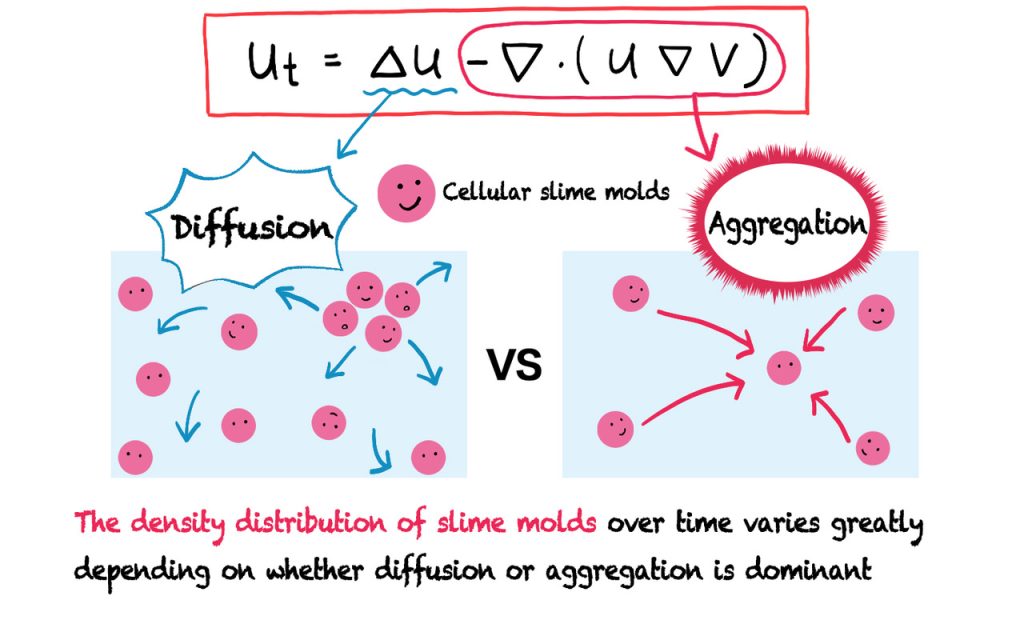
What makes the Keller-Segel system fascinating is that it contains two key terms: one representing diffusion and the other aggregation. The behavior of the function describing the slime mold’s density over time depends on the balance between these two effects. For example, when the aggregative force dominates under certain conditions, the slime molds cluster together, causing their density to become infinitely large at a single point —a phenomenon known as a blowup. Conversely, when diffusion prevails, such a blowup does not occur. So, what kind of behavior will the system exhibit?
-I investigate the mathematical structures underlying these dynamics and publish my findings in academic journals.

What inspired you to study the Keller-Segel system?

At the end of my first year as a master’s student, my supervisor, Professor Tomomi Yokota^*1, asked me, “What kind of research are you interested in?” Professor Yokota encouraged his students to participate in mathematical workshops and academic conferences actively. Listening to many of the talks there sparked my interest in biological models. When I told Professor Yokota about this, he immediately reached out to Professor Yoshie Sugiyama^*2, who was conducting active research on the Keller-Segel system, and invited her to give a lecture at the study group. This lecture became the catalyst for my research on the Keller-Segel system.

At the time, I was still in my first year of the master’s program, so I probably didn’t understand much of what Professor Sugiyama was saying. However, I vividly recall her joyful and lively lectures. Seeing her so genuinely enjoy mathematics filled me with admiration and may have inspired me to start my own research.

*1: Professor at the Faculty of Science Division I, Tokyo University of Science, with a research focus on analysis (partial differential equations) (as of May 2025).
*2: Professor at the Graduate School of Information Science and Technology, The University of Osaka, specializing in nonlinear partial differential equations (as of May 2025).

During my master’s and doctoral studies, I focused on analyzing quasi-linear diffusion Keller-Segel systems. In particular, I worked on a conjecture concerning the balance between diffusion and aggregation that determines whether a solution exists globally in time. It was a process of continual trial and error—each small step forward, even a tenth of a step, felt like real progress. I still clearly remember the day I finally saw a path toward solving the problem using an evaluation method known as maximal Sobolev regularity.

After proving the existence of a global-in-time solution, I went on to explore new questions such as:

• Are the solutions bounded, or do they blow up at infinity?
• To what functions do they converge over time?
• And under what balance between diffusion and aggregation do solutions blow up in finite time.

Each of these studies was compiled into papers and published in international journals.

Modeling cancer cell spread with partial differential equations

What can you tell us about your other research?

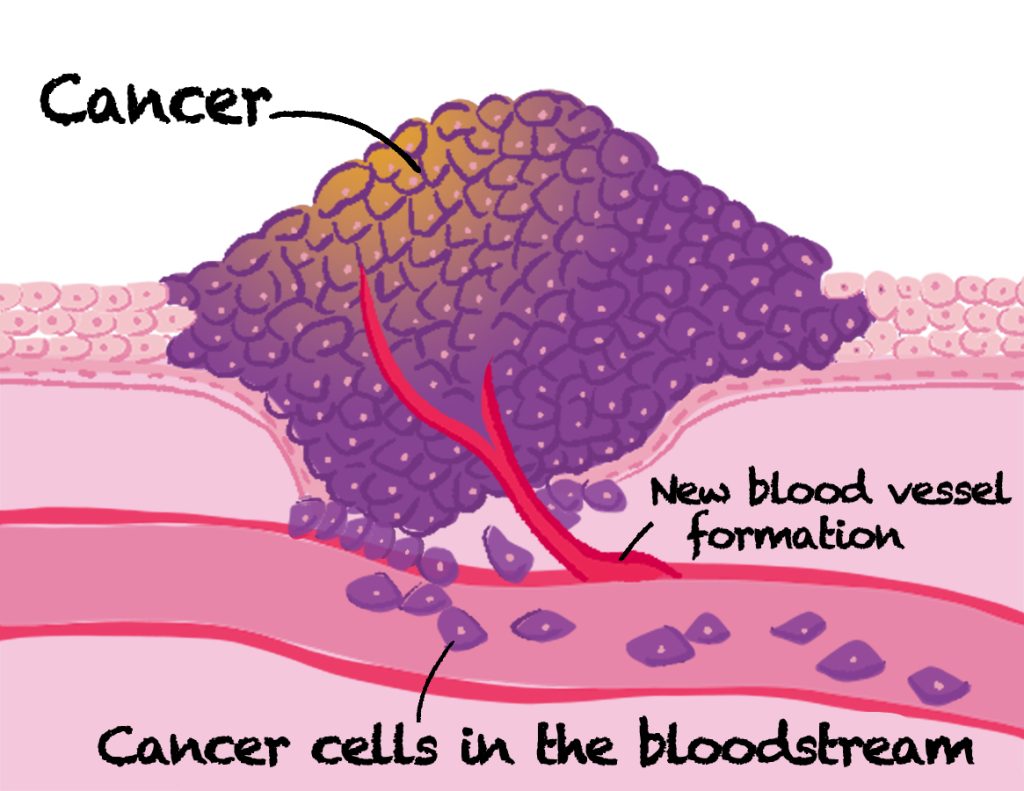
My second research focus is on a partial differential equation that models how cancer cells invade surrounding tissue, known as the ‘cancer invasion model.’

Cancer cells secrete proteolytic enzymes, which allow them to gradually move into and degrade the surrounding normal tissue—a process called invasion. The model I study is based on the hypothesis that the action of these enzymes produces new substances that attract cancer cells, thereby enabling more efficient invasion.

The cancer invasion model is a system of coupled differential equations, similar to the Keller-Segel system, with a ‘diffusion term’ and an ‘aggregation term.’ However, it involves four equations instead of two, making the analysis significantly more challenging. Interestingly, the balance between diffusion and aggregation differs from that in the Keller-Siegel system, which I find extremely fascinating. Even now, my collaborator, Professor Yokota, and I meet almost every week at the whiteboard to discuss these problems head-on.

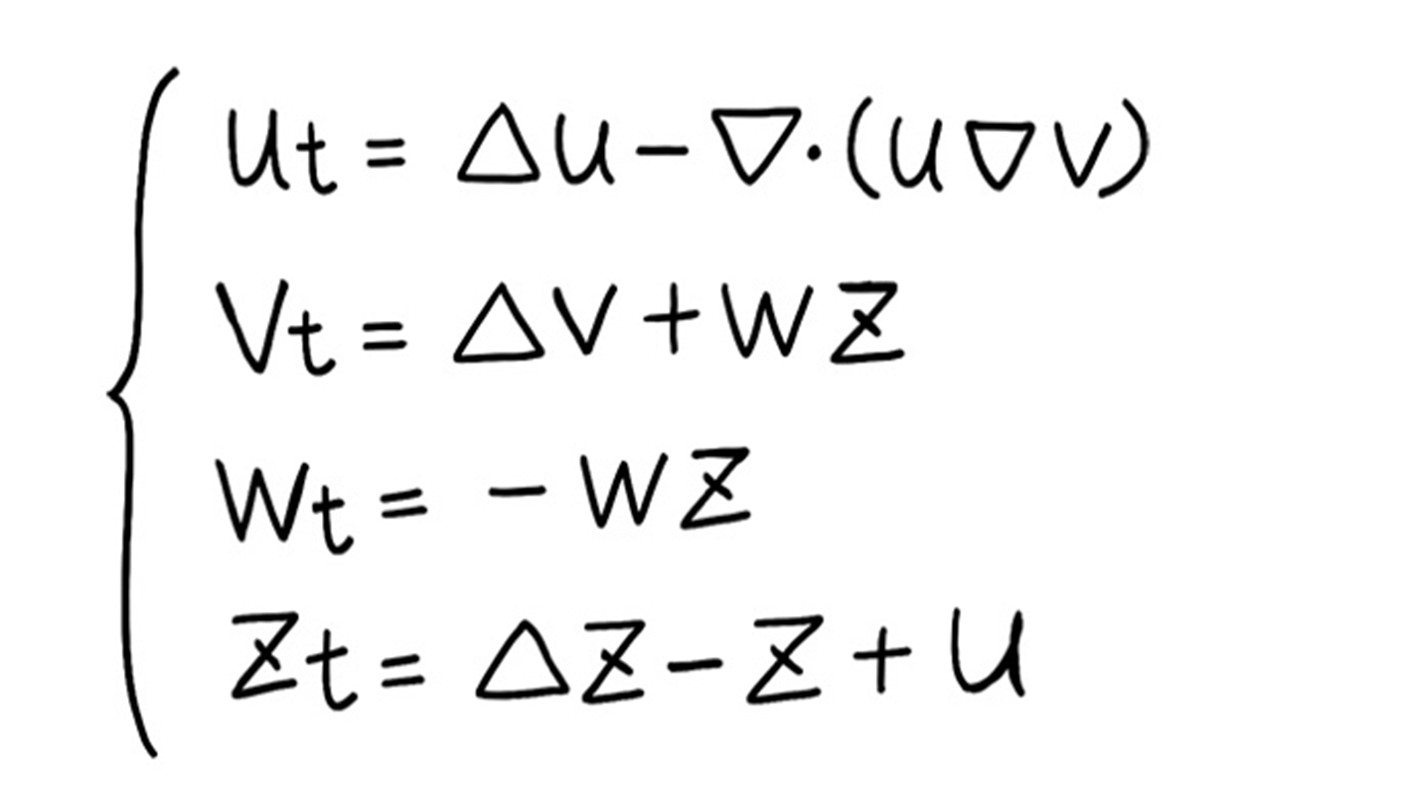
“I can’t let my studies end like this,” she thought—and set out on the path to becoming a researcher.

What led you to pursue a career as a mathematics researcher?

Originally, I had planned to become a high school mathematics teacher after graduating from university. The turning point came during a seminar I took in my third and fourth years. Through that seminar, I found the joy of gradually understanding things I had previously struggled with. At the same time, I realized that what I had learned at university so far was only a small part of the vast world of mathematics. “Mathematics is far broader and richer than I ever imagined—and I’ve only just begun to explore it,” I remember feeling that I couldn’t possibly graduate without delving deeper and achieving a true sense of accomplishment in mathematics. That feeling led me to pursue graduate studies.
During my time as a graduate student, I was fortunate to study in a supportive environment. Under Professor Yokota’s guidance, we held student-led seminars with lab mates, and senior students generously spent long hours discussing mathematics with us.

Mathematical research is never-ending. As I progress in my work, new questions and ideas constantly arise, and sometimes even questions from research presentations spark entirely new challenges. My mind is always filled with research themes I want to tackle, and I approach each one carefully. It’s deeply satisfying when I find a clue that leads toward a solution—and when I finally solve a problem that has been troubling me for a long time, I feel so happy I could almost jump for joy.

I heard that you also organize international research conferences.

Yes, I  host an annual international research conference, inviting researchers from around the world who have made significant contributions in the field of chemotaxis models—a general term that includes models such as the Keller-Siegel system and cancer invasion models. In 2022, the conference was held in Germany, in 2023 in Japan, and this year in Italy (as of May 2025). While the administrative work can be tedious, I am always grateful when speakers agree to present, and I find their talks extremely educational. We are currently working hard to find ways to attract as many participants as possible. This type of international exchange can sometimes spark new research themes and collaborative projects, so I hope to continue this initiative in the future.

Deeply Engaging with Mathematics: Building Strength for the Future

Looking ahead, are there any areas where you hope to explore through collaborative research?

I would like to collaborate with researchers who conduct numerical simulations of partial differential equations. I typically analyze these equations mathematically using only pen and paper, but I believe that running approximate simulations on a computer could provide new perspectives.

Finally, what message would you like to give to students?

“Take your time and think deeply about mathematics”—I believe this is the most important thing. For example, when reading a textbook, don’t just skim through aimlessly; read every line carefully, and consider even what’s implied between the lines until you fully understand it. If something is unclear, it’s best to clarify “how much you understand and where you’re confused” before asking a question, as this will make discussions much more fruitful.
It will take time, but the experience of engaging with mathematics in this way will become a valuable asset. I am still only halfway there myself. Let’s tackle mathematics together, step by step.

● ●　Off Topic　● ●